PharmIV
This respository supplies the tools necessary to calculate the power of an instrumental variable analysis study using a single binary instrument Z to analyse the causal effect of a binary exposure X on a continuous outcome Y in the context of pharmacoepidemiology. If you use this material, please cite:
Walker VM, Davies NM, Windmeijer F, Burgess S, Martin RM. Power calculator for instrumental variable analysis in pharmacoepidemiology. Int J Epidemiol. 2017 Oct 1;46(5):1627–32.
The simulations and plots included in this paper were produced using Stata and the code can be found in the folder ‘Stata_paper’.
Shiny
The folder ‘Shiny’ contains the code to produce the power calculator shiny app. The app is avaliable at:
https://venexia.shinyapps.io/PharmIV/
R package
The folder ‘R_package’ contains the power calculator R package.
Installation
The package can be installed using the following commands:
install.packages("devtools")
devtools::install_github("venexia/PharmIV", subdir="R_package")
Syntax
The syntax for this package is as follows:
PharmIV(n = NULL, delta = NULL, alpha = 0.05, sigma = 1.00, prob_x1 = NULL, prob_z1 = NULL, cond_z1 = NULL, cond_z0 = NULL)
Example
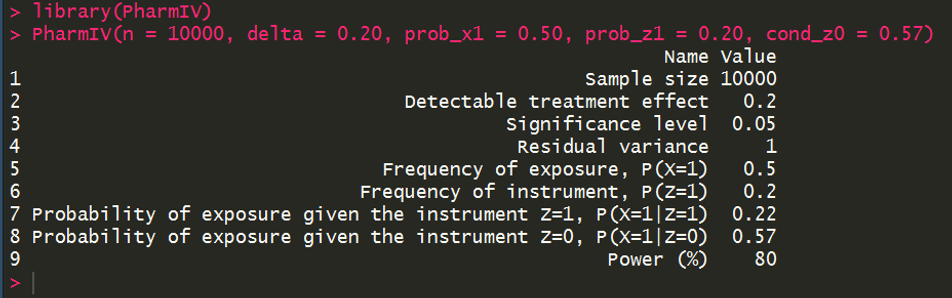
What is the power of an instrumental variable analysis study with 10,000 participants to detect a treament effect of 0.20 for a treatment with a frequency of exposure of 0.50? The binary instrument for the study has a freqency of 0.20 and the probability of exposure given the instrument Z=0 is 0.57.
Stata package
To allow web download, the power calculator Stata package is contained in its own repository:
https://github.com/venexia/PharmIV-Stata
Installation
The package can be installed using the following commands:
net install github, from("https://haghish.github.io/github/")
github install venexia/PharmIV-Stata
Syntax
The syntax for this package is as follows:
PharmIV, n(numlist) delta(numlist) alpha(numlist) sigma(numlist) prob_x1(numlist) prob_z1(numlist) cond_z1(numlist) cond_z0(numlist)
Example
What is the power of an instrumental variable analysis study with 10,000 participants to detect a treament effect of 0.20 for a treatment with a frequency of exposure of 0.50? The binary instrument for the study has a freqency of 0.20 and the probability of exposure given the instrument Z=0 is 0.57.
